You can also download a PDF version for Adobe Acrobat (170K), although I'd recommend downloading the picture of the Walsh functions as well, since it didn't compress particularly brilliantly.

"Of course, the thing which makes it all possible is this." The professor held up a strange looking black box. Inside it were two clamps affixed to opposite sides: one held a powerful torch, which was shining at what the other clamp held - a small electronic chip.

"There it is. A light dependent existor, or LDE. Taken years of research that one has."

Richard stared at it closely, and wondered what the professor had invited him to the lab for. If you could call it a lab, he reflected. It definitely wasn't one of those nice Victorian physics labs, with lots of old, aesthetically pleasing pieces of wooden equipment lying around, about whose use nobody had a clue. Nor was it a brand new modern lab, with lots of impressive-looking pieces of shiny white plastic equipment lying around, about whose use nobody had a clue. Nor was the room actually more than twelve feet square. What it did have, however, was an awful lot of black boxes lying around, occasionally piled up to the ceiling. Wires were strewn around the floor and workbenches. A couple of torches, a large box full of Duracells and some electronic scales also graced the room with their presence. Richard had a nasty feeling, much to his unease, that the professor knew exactly what they were all for. And he had a nastier feeling that he, Richard, would also have a vague idea about them thrust upon him by the time the day was out.

"Well, of course, now I've cracked this problem, I should have the whole project wound up in about a year's time. All I've got to do is find a way to make them smaller. And put in the fibre-optic routing system. That'll be fiddly."

Richard decided to brave it. He was, after all, a mathematics lecturer with a rather good track record despite having an ostentatiously clean-shaven chin and a normal haircut, and was not averse to a little physics here and there.

"What, exactly, are you trying to do?" he asked the professor kindly. "I mean, start from the beginning. I'm not really sure what a, er, what was it? A light dependent existor? Hmm? Yes, what one of them is."

"Well you see, it rather began, I mean actually began, when I found this short student essay a few years ago. Well, it must have been written a good few years before that, but there was no cover sheet to tell the date or the author. Just two pages of badly typed text. Here." Richard was handed some crumpled sheets, which he proceeded to read.

"So there you have it," said the professor as Richard handed the papers back. "Of course, it took a little while. You can't just make an antinomialist computer overnight. In fact, I still haven't been able to make it invisible. But with the use of this..." A wave was directed at the box. "I can at least make it conform to the basics. Obviously, with something as seemingly impossible as this, you build something you think will work, and it doesn't. You don't know why. Most of these black boxes do indeed appear to be antinomialist computers, but unfortunately only from a behaviourist point of view: you put something in, the right thing comes out. Open up the black box though, you find it's simply cheating - like congratulating the computer on winning the Turing Test only to discover there was a person behind it all the time. Of course, the failures helped me to understand the problem. But this..." The box was waved at again. "This is the real thing. This will let me build a computer which calculates, not just by making electricity run round a maze of transistors, but by making the very existence or non-existence of those transistors integral to the workings of the chip."

It would be an overestimate to say that Richard was amazed. He was not for one minute caught up in the enthusiasm of this person standing in front of him. After a slight pause, he offered his entire collection of thoughts on the subject to the professor.

"Huh?"

"It was certainly hard going at first," the professor explained. "I mean, how, logically, do you make an invisible computer? And then it hit me.

"If something doesn't exist, then it can't be seen, and therefore can be used to hold the variables that antinomialism is so keen to get rid of. But, of course, this gives rise to a rather more intractable problem: how to make something non-existent. More to the point, how do you control its existence? It was flicking through a book on geometry that gave me the answer to the latter. You know, I presume, what a star-shaped room would be in mathematics?"

"Yes," replied Richard. "A star-shape is one where there is a star-centre, from which every point in the room can be seen."

"Exactly. But it would be easier to describe in laymen's terms as a room whereby every point in the room could be lit by a lamp placed in a specific spot: the star-centre, as you say. Thus a circle, or any convex polygon, would be star-shaped. However, there are plenty of shapes which aren't star-shaped, and therefore couldn't be lit by a single lamp.

"The obvious way round this is with mirrors. Indeed, if you turned every wall of your non-star-shaped room into a mirror, most people would assume that you could then light the entire room. But there are exceptions. This is the most well-known example of the so-called 'Unilluminable room'."

The professor picked up a pencil and a pad of paper, and proceeded to draw a diagram.

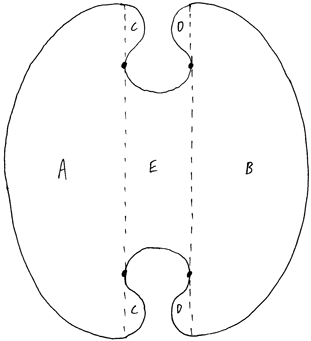
"Now this may look like a complicated shape, but in fact it's simply an ellipse split vertically down the major axis - the dots are its foci - and any shape you please in the middle so long as it touches (and doesn't go beyond) the major axis at each focus. Now, because ellipses have wonderful reflective properties, for instance light from one focus always being reflected through the other, any lamp in part A cannot light parts D, even if every wall is a mirror. Likewise for lamps in B not being able to light C, and a lamp in E cannot light either C or D, nor can a lamp in D light A, C or E.

"Of course, you may ask why all of this is necessary. Indeed, it's a question I've asked myself on many an occasion. However, it seems to work."

"What seems to work?" asked Richard. "I know you mentioned something about a light dependent existor, but if it's what it sounds like, then surely just putting one in a box with a controllable light source would work."

"That's what I mean. I thought I'd explained that you can't do these things overnight. Of course putting one of these in a box and closing the lid will make it vanish, and opening the lid will make it exist again..."

At this point, Richard suddenly got terribly worried about the whereabouts of the professor's marbles. Here was a person who was an eminent physicist getting all philosophical about whether things exist when you can't see them. Leave those sorts of problems to the philosophers, thought Richard, and good riddance to them. Of course, it all hinged on your definition of existence. Or indeed your definition of sound if you started talking about trees falling in forests. He realised his mind was starting to wander, and suddenly snapped back into concentrating on what the professor was saying. "...so you simply can't make a computer out of it. What's more, this bent ellipse offers many, many more possibilities. For instance, imagine a room of that size and shape and about, say, 1cm high, with three fibre optic cables coming in vertically at A, E and B, with rounded ends so as to distribute the light. A fibre optic also comes out of the bottom of the room exactly opposite the incoming E one. Then place two LDEs in the room - one in either of the C corners, and one in either of the Ds. And there you have it. Light can pass straight through the room via the E cables without making anything exist, and if you take that as a possible 'result' then every combination of the three incoming lights (eight in all) gives a different result. Then all you do is connect lots of these together and make the existence of light in other fibre optics dependent on the existence of the LDEs. Simple. The whole lot coagulates into a large neural network, and you can start to lose variables with the flick of a switch. The switch being on a medium sized torch, of course. And whereas most computers need a crystal for their internal clock rate, you simply set a couple of these to feed back on themselves, so that the existence of an LDE induces its own non-existence, and vice-versa. It could go much faster than 300MHz if you got them efficient enough."

Richard took a deep breath. Efficient enough at not existing? He suddenly realised the basic problem he had with the whole concept, and was surprised that it hadn't grabbed his attention earlier.

"How," he asked, "exactly, does a light dependent existor work?"

"Ah, you're asking what has taken me three years or so to discover. It is a little complicated, so I'll only explain the basics to you, since you're just a mathematician." The temperature of the lab rose slightly as Richard seethed. "You no doubt know of Schrodinger's cat. Of course, everyone does, along with the butterfly effect and Fermat's last theorem. The problem is, not everyone understands these things, and some even start asking why we're not out there trying to catch the damn butterfly. But basically, with Schrodinger, the question arises: is the cat dead or alive? No-one stops and thinks about whether the cat actually exists. But it's actually much simpler to think of that - philosophers have worried about it for centuries, so there's a definite head-start there. They've always wondered whether their own furniture stops existing when they, the philosophers, leave the room. Generally doesn't worry the furniture, of course, but the principle's there. So all you have to do is find a substance that is so unstable at the quantum level that, to put it in laymen's terms, if it thinks it can't see itself, it decides it doesn't exist any more. So if there's no light around, it stops existing. Make an electronic chip out of it and you've got a sort of Schrodinger's cathode, if you like.

"Now, if you make something useful out of this substance, for instance a chip which is a control for a sort of switch on a fibre optic cable, then you have what you see before you. Look."

The box, rather than being waved at, was placed on the electronic scales. The lid was firmly closed, and the torch switched off. The value on the scales completely failed to change. Richard raised an eyebrow.

"That's the problem, you see. Something has to stay in existence to work out if the light has been switched back on. And although the chip disappears, whatever remains, despite not being there, weighs the same."

"I can see how that might be a problem" said Richard. "Though I think I'm beginning to understand all of, er..." The box was slightly taken aback at being waved at by a different person, but it decided on balance to put up with it. "...this stuff. I think, however, that even you can guess what I'm going to be sceptical about." The temperature rose again as the professor's exothermality caught up with Richard's.

"Whatever remains to check the light level isn't capable of holding variables in its memory," said the professor reassuringly. "So the computer is still fully antinomialist." Richard frowned. "Oh, how do I know the LDE's vanished? In the beginning I put a camera in the box and took a flash photo. You see, in the earlier versions the chip was very inefficient, so it took a relatively long time for it to notice that the lights had come back on. "However, as the chips got more efficient, I came up with the idea of viewing the chip with ultrasound - it's easy to see whether anything's there with ultrasound, and whereas the Schrodinger's cat experiment relies on nobody looking into the box at all, this simply relies on not letting the chip see itself. So I can "view" the chip with no problems whatsoever. Unfortunately, they took back the ultrasound equipment, needed it for something else apparently. But it doesn't matter, now I know the basic principle works all I have to do is make it smaller and find a way of connecting them all up."

Richard was starting to get interested now. "How small are they going to be? How are they all going to be connected? I mean, how do you decide where a fibre optic goes once it's been switched on? Have you thought about that? It's going to be tricky, isn't it?"

"Yes, of course I've thought about it. But you're right, it is going to be very tricky. Fibre optics can be a fraction of a millimetre across, so the size of these 'rooms' could be as little as one or two millimetres in length - that is if the mirror coating is accurate enough at that kind of size. But that shouldn't be a worry. No, no, the main problem is indeed going to be how to connect them up. Obviously if one is going to try and store the variables in these LDEs then there has to be some kind of controlling chip that handles the input from a keyboard, but after that, well, I've only got as far as designing the clock and the logic gates." The professor brandished the pad of paper again, and flicked through it.

"Here we go. You must understand that I've had to invent a new symbol for these things - if you imagine the previous picture as a plan view of the room, my new symbol is a sort of side-on view. The flat side is like the top of the room - it has the three inputs into it, the outer ones being the optic fibres to areas A and B. The other side has two bumps - these are purely symbolic, as the room obviously has a flat floor. Each of these bumps has the output for one of the two LDEs in the room. Of course, these outputs are not fibre optics but simply switches, hence they end in an arrow which touches an optic cable. Each bump contains a '+' or a '-' sign: a plus mean that the output switch allows light through when the LDE exists and stops light when it doesn't, and a minus means the switch doesn't allow light through when it exists and does when it doesn't. Understand?"

"I think so. Let me have a look, I'll see."

"Oh, of course, the middle fibre that goes straight through the chip is represented by..."

"Yes, what's the point of that 'straight-through' bit?"

"Simplicity of wiring," replied the professor. "It often reduces the number of times fibres have to cross. Anyway, the output fibre is represented by a line coming out of the thin bit between the two bumps. Oh, and a continuous light input is represented by a double arrow on a line. I've also put single arrows on some lines to try and make it a bit more obvious where inputs and outputs are, and I've also assumed that when a fibre splits in two, each fork ends up with half the light level in it, and vice-versa when they join.

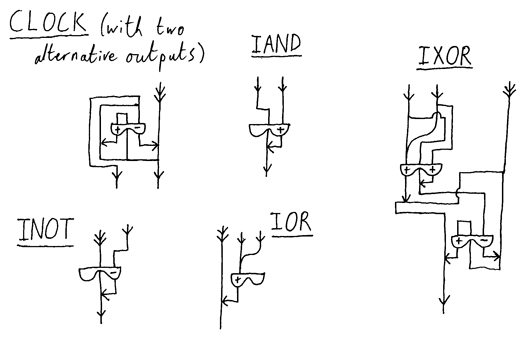
"Now, the clock's a bit complicated. If you say that it takes an LDE 1 unit of time to realise that its existence should have changed, then if the moment the torch is switched on is t=0, the status of each clock output looks like this:

"So all you need to do is take both of them through an invisible exclusive OR (IXOR) gate and you've got a clock that flashes light out every other unit of time."

Richard was now completely flummoxed. Was the professor really taking all of this seriously? He could have understood if it had been some normal aspect of physics or mathematics, but building antinomialist Boolean logic gates for semi-existential computers that would in the end allow all usable numbers to be disposed of was not really what he wanted to hear of a morning. Morning? Richard realised it was past noon, and thought perhaps raising the subject of lunch would be a good idea. He did so.

"Hmm?" asked the professor. "Lunch? Well, why not. I'm afraid I rather fancy something hot today. Shall we go to the pub?"

It was the summer holidays, which brought two advantages. Firstly all the lecturers could actually get on with some work without having a load of horrible students around to bother them, and secondly it was meant to be warm. Unfortunately the latter had decided not to exist today, and a damp, steady drizzle fell from a depressingly uniformly dark-grey sky. Two figures walked as quickly as their spirits would allow them to the pub around the corner, which tended to do nice food. At least, nice as far as pub food went.

"So what are you doing other than this computer these days?" asked Richard once they had settled with their pints.

"Well, the other day I put the finishing touches to another black box I've been working on. Should be quite a good one - it makes things work modulo n. As in zero up to n-1, since it works with addition."

The professor was definitely mad, Richard decided. Why this persistence in making these black boxes? What possible use were they? Or rather, were they possible?

"It's the most efficient way of making a vacuum I've ever seen," mused the professor. "Just set it to reduce mod 1 and switch it on."

"You mean if you set n=7 and put eight marbles in, you open the lid to find just one marble left?"

"Yes. Most of it was surprisingly easy to build, actually. The trickiest bit was insulating the box well enough to ensure the field never extended into the room. It got quite nerve-racking at times."

"But where do they go? And how does it know if two objects are the same? Number theory is definitely in the Pure Maths category - it's not really susceptible to real-world analogies, let alone real real-world analogies."

"Not at all, not at all. There's obviously some rather complex physics involved in the workings of it, but it definitely works. I suppose I could explain some of it.

"Plato was involved in quite a bit of mathematics, but possibly the most important thing he did was to lay down once and for all the idea that new theories in maths are discovered rather than invented. Over the centuries, and especially since Newton, people have tended to agree with this, since so much maths is used in describing the real world. Obviously, if maths is continually being invented, why should it help to describe something which existed well before us?

"Unfortunately, this rather raises the question of where all the mathematics is before we get around to discovering it. Plato answered this by saying all the maths hung around in a special heaven, along with the perfect geometric shapes."

Richard thought about this in the light of the student essay on antinomialism. A frown crept across his face. "However, Plato went one step further, which I always reckoned was a sign of him being a bit mad. He started branching out into philosophy, and asked: 'how do we know to call a table a table? What, exactly, are the set of specifications by which we know that a chair is a chair and not something else entirely?' It's quite a tricky one once you start to think about it.

"So Plato decided that the best answer was to have a heaven, a Platonic heaven as we now call it, which would contain the perfect everything - the blueprints from which all earthly objects were made. Hence a table is a table because it is an imperfect copy of the perfect table in Platonic heaven. Which is of course rubbish, since it would take some damn cunning axioms to stop it containing all of the perfect imperfect tables. And the perfect imperfect-copies-of-the-perfect-imperfect-tables. And so on."

Richard took a deep breath of the slightly smoky atmosphere and a long sip at his pint. He also wondered when the professor would shut up so that he could go to the bar and order some food. Just a bacon butty and chips, he decided, would make the afternoon bearable. He took another drawn-out sip, and released a frown which he realised had been gradually deepening for over a minute.

"However, it would appear that there must be at least a speck of truth in Plato's theory," the professor continued. "For it turns out that when you make a load of molecules into an object, something changes at the quantum level in each and every particle in each and every molecule to reflect what the object is. A kind of universal barcode, if you like. It explains a lot if you think about it. Like why antiques and buildings often seem to retain a flavour, a sort of smell, of what they've been through, what they've been made into. Anyway, once I'd worked out how to tap into this, er, quantum smell if I can call it that, making a modularity field was easy."

Richard saw his chance and pounced.

"Amazing," he said, smiling widely. "What can I get you to eat? I think there's some sort of generic pie masquerading as today's special."

"Just soup, thank you. Any flavour that looks nice and whose recipe sounds hard to get wrong."

"Righty-oh," said Richard. He went to the bar, ordered onion soup and his own bacon butty, and meandered back to the table thinking about his own work. He didn't have much to do at the moment, and could probably afford to be distracted by the professor for a longish lunch. Just that small group theory result, he thought, and the holiday's work was nearly over. Apart from actually writing up the paper, but that wasn't really urgent. It occurred to Richard that he had spent many years researching hard and interesting mathematics, and had in the process got a fairly thorough knowledge of the field; and yet he was beginning to be convinced by the professor's dubious ramblings. He got back to their table and sat down, resolving to broaden the subject of conversation into something more everyday.

"Extortionate," he exclaimed. "The cost of food in this pub. They probably won't even cook the bacon enough to make it crispy."

"Hmmm," replied the professor. "You know, Douglas Adams, I think, had a theory. He said that mathematics works differently in restaurants, purely on the grounds that the bill never adds up to what you actually ate. This is clearly nonsense - bills don't add up in restaurants for the simple reason that everyone's had too much wine. No need to start bringing special theories about artificially-induced fields where mathematics works incorrectly. Or rather, differently."

Richard forgot his resolution instantly.

"You seem to be quite into that sort of thing, though."

"I'm a physicist, not a mathematician. If creating a black box in which maths works differently is a by-product of some new discovery in physics, then so be it. But you're meant to be the one that comes up with new theories in maths, not me."

Richard sat in silence pondering. The professor picked up a newspaper that had been left lying around, and seemed to be content reading it. Richard waited a politely article-finishing length of time, and struck.

"You seem to be more of a philosopher than a physicist, though. I mean, here you are talking about Plato and how his ideas run to the heart of quantum mechanics as if such thoughts were everyday occurrences in the life of a physicist, but they're not."

"I'm merely an amateur philosopher," replied the professor, calmly folding the paper and placing it on the table. "I take ideas that I read about and come up with other ideas more in keeping with my subject. You could do the same if you read a few books and trained your mind to think in the right way. Who knows what new discoveries you could come up with. Take the antinomialism essay - it mentions Wittgenstein's 'Tractatus'. Read more of it than is quoted, and you start coming across bits like 'The existence and non-existence of states of affairs is reality'. That kind of thing helps me discover things - how else would I have had the confidence to persevere with the LDEs?"

"I don't need to read books to think of some things," replied Richard in an unnecessarily defensive tone. "For instance, I can already see a problem in this 'universal barcode' notion of yours. From what you've said, an object is defined as something specific because it was made as something - its maker, or the fact that it naturally formed, literally made it what the quanta claim it is. But an object doesn't stay the same forever. Is an old clapped-out chair the same as a new one? Is a mug that has always had tea sipped from it the same as one from which coffee has always been drunk?"

"You know," came the reply, "that we as humans share a staggering percentage of our genes with the lowliest of bacteria. Almost one-hundred percent of our genetic code is the same as other mammals', especially the apes. We are all living creatures, so we share some of a common pattern - the more alike, the more we share. The state that the quanta adopt to reflect the object they make behaves in a very similar manner: very alike objects, for instance your two mugs, would have an almost identical code. I think you understand, yes?"

Richard looked puzzled. "How accurately can you read this code? Estimates vary, but it's generally assumed you can't measure someone's DNA to more than about 2,000 - 10,000 variations."

"I don't know. After a bit of experimentation I realised that it was easy enough to put a dial on the side of the box that would determine how similar two objects had to be to count as the same, but I never really put much thought into it."

Richard considered the possibilities, and ended up looking even more puzzled. He couldn't work out why the professor hadn't thought more deeply into it before. There had been some mention of an object's life being contained in some sort of quantum smell, but when you consider the practical implications, surely there were an enormous number of uses for something that could accurately determine what had happened to an object simply by placing it next to several objects which had had similar lives and reducing modulo 2. The disadvantage being of course that your object would disappear. But it all depended in the first place on how accurately you could read the code. More importantly, he realised, it depended on coming up with a decent test to see how accurate you could go. Richard drank deeply from his pint, and settled into thought. The professor picked up the paper again.

Richard abruptly came out of his thinking to find a waitress standing by the table with their food. After a brief explanation by Richard of whose was whose, the soup and the bacon were set down along with some napkin-wrapped cutlery. The professor put down the paper, sipped the soup and started to butter a bread roll. After a moment's thought, Richard tucked into his lunch as well.

He was half-way through, and had just finished his pint, when he spoke again.

"If we could get your modulo box to be accurate enough, we could break one of the most fundamental laws of probability."

The spoon paused on the way between bowl and mouth. "How do you mean?"

"Well," carried on Richard. "If we threw a ten pence piece and got a head, then threw another ten pence piece and got a tail, then the two could be distinguished."

"Only theoretically," said the professor, letting the spoon rest back in the bowl. "They would have had such a different life before we threw them that any difference arising from the way they landed would be swamped by the previous ten years of differences."

"Is there no way of isolating the particular change? To go back to the human genome analogy, we know the genes that cause certain features like eye colour. Is there no way of doing the same thing with objects?"

"There may well be." The soup finally made it to the mouth as the professor frowned in thought. "But it would take several years to work out exactly which change corresponded to the throw. And anyway, I don't quite see what you're driving at with regards to changing probability theory."

"I suppose you're probably right. I was wondering if it would be possible to bias a coin purely on the grounds of what had been thrown before - ten heads in a row makes it much more likely to get a tail next time, that sort of thing. But even if you could measure how the coin had been thrown, it would be difficult to induce the probability of it getting a head."

"Not necessarily. It might be possible that the 'genetic' quantum make-up of an object also determines what it's going to do in the future. However, that would be a decisive victory for determinism, so it probably isn't right. We can't have quantum physics proving the clockwork universe theory."

"No, I see what you mean," said Richard. "We used to have a similar view of things at school and in undergraduate days. It was called the 'Easy Answer Theorem', and stated that if the answer to an exam question was slightly too long or ugly for comfort, then it wasn't right. It usually works in real maths as well. It's quite amazing how many results are extremely elegant. I suppose it goes back to the Perfect Maths in Heaven idea."

"Actually," said the professor after another spoonful of soup, "that reminds me of some essays Stockhausen once wrote. He thought that mathematics applied to well-rounded music in an extremely deep manner. Not only to his own music, in fact, but also to that of Bach and Mozart."

"You mean Stockhausen the composer," interrupted Richard. "The one who was big in the sixties for doing strange electronic music?"

"Yes. He put an awful lot of maths into his music. He was the first one to realise that if one is going to write a piece of music where pitches are represented by the tempi and duration of the notes, as many had tried before, you have to make the tempi logarithmic rather than linear; just like in pitches where an octave up is double the frequency rather than adding a fixed number. So he wrote 'Gruppen', which has three small orchestras each with their own conductor, playing in logarithmic tempi. It's fantastic to hear live. But I digress...

"When he was young and didn't know any better, he wrote several essays on how mathematics can be used to decide what overall structure a piece of music has. Generally these were about where cadences occurred, but later on he decided on using the phrases 'the frequency domain' and 'the time domain' as how we perceive both pitch and structure. His idea was that if you take a note, say middle-C, then whatever the timbre, its pitch is defined by the frequency of the sound-wave, in this case 256Hz. Go down an octave, its frequency is 128Hz. Keep going, and when you get below 15Hz, the ear stops hearing a pitch: thus we're out of the frequency domain and into the time domain. It's all to do with our perception of things. Anyway, once you're into the time domain you can start talking about the structure of a piece of music, hence his 'duration octaves' and suchlike serialist devices."

"Serialist?," asked Richard.

"Yes, you know, serialist. Where you take a set of numbers - derived, say, from a series of notes and assigning a number to the pitch of each - and then generate everything else in the piece from that set and transformations of the set. Tempi, note duration, dynamics, everything can be decided from the original numbers. It was terribly fashionable for a while, although it did tend to spawn all the usual 'my 5-year-old could do better' rubbish."

"So what he was saying is that our perception of time is logarithmic, like pitch?"

"Yes. Although he never phrased it quite like that."

"And do you believe him?" Richard's brain was starting to explore the possibilities of this. "If he's right, and the frequency and time domains are basically the same, then it sounds like something interesting ought to happen."

"It's not a case of believing or not believing. If you follow the thing out to its logical conclusions, so to speak, well, you're right. Interesting things do theoretically happen. Fourier analysis, for instance."

"Fourier analysis on time?"

"You can analyse any sound, any timbre, and get its component frequencies - obviously this is possible, since the set of sines and cosines of multiples of x form a basis for all possible periodic functions. Once you have the Fourier analysis of the sound-wave, you know its pitch, i.e. its frequency, and its harmonics. Once you're into the time domain, however, you stop thinking in terms of frequency and start talking about time itself. Not that Fourier analysis of time is particularly useful, of course. You end up with notions of 'time harmonics', which no-one really wants to have to deal with."

The professor went back to eating hunks of bread roll dipped in soup. Richard, with a bacon butty still half-way between plate and mouth, thought for a moment. "Fremder," he said. "Russell Hoban."

"Sorry?" said the professor.

"Fremder," replied Richard, taking a bite and chewing. "It's a Russell Hoban novel. One of the things in it is that they discover that time works like film, in frames with gaps in between. So they invent a 'flicker drive' which can get them to any place in the universe in between the frames - basically doing trick photography down the gaps."

"Does this help us?" asked the professor.

"Well, it's just that Fourier series aren't the only way of breaking down periodic functions."

"Well, of course, there are an infinite number of bases that generate real functions."

"Ah, but some of the bases involve square waves."

"None of them contain purely square waves, though," said the professor smugly. "I read this somewhere. Rademacher came up with the idea as far back as 1922, but you can't generate arbitrary functions from a fundamental square wave and its harmonics at powers-of-two times the fundamental frequency."

"True," said Richard, warming to the subject, and not for the first time. "But also in 1922, a guy called Walsh came up with really weird square waves. I'll draw the general idea for you."

Richard grabbed a beer mat, pulled a pen out of his pocket, and started to sketch while the professor looked on in interest.

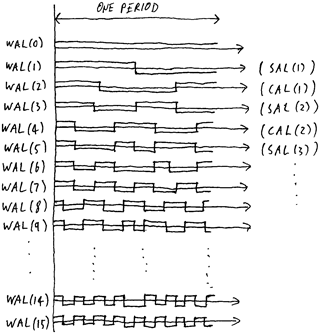
"You can see here that the first proper Walsh function, marked Wal(1), is a basic square wave, or Rademacher function, of period one. Then Wal(3) is the next Rademacher, of period a half. Then Wal(7), and it goes on with Wal(15) being the one after that. In between are slightly odd waves, which can be generated from Rademacher functions by means of something called 'Gray's code' and exclusive OR gates. It's all quite hard, especially if you're only a physicist, but you end up being able to analyse functions, all periodic functions that is, in exactly the same way as Fourier analysis; it's even gone as far as Wal(even n) being called CAL(n/2), for Cosine wALsh, and similar for Wal(odd n) being called SAL((n+1)/2)."

"Now, now hang on," said the professor hastily. "You're not suggesting that time can, well, be broken down into fundamentals and harmonics that rapidly alternate between two states? Positive and negative time? Compression and rarefaction of time?"

"You're the one that suggested time could be analysed like sound," replied Richard. "I'm just the mathematician."

The professor frowned, and went back to mopping up the last of the soup with the bread. Richard popped the last bit of butty into his mouth and finished his drink. He noticed that the other glass on the table was also empty, and hoped the professor might think of buying the next round. He did not have to wait long.

"Ah, you've finished. Allow me." The professor got up, picked up the glasses, and wandered over to the bar. Richard glanced at the newspaper, decided it was probably not one he'd find pleasure in reading, and went back to thinking about what had been said about studying philosophy.

I do read books, thought Richard to himself, and plenty of them. Mainly mathematical ones, he reflected, but mathematical logic was basically philosophy, wasn't it? To Richard's surprise, a lot of what he'd read came creeping back to him: all the strange and twisted theories and ideas he'd never really thought about much suddenly appeared to have new meaning. The professor was coming back with more drinks, and Richard went on the attack.

"Do you know the basic principles of mathematical logic?" he asked.

"Well," said the professor putting the beers down on the table and taking a seat. "I know them roughly. Probably not to the letter. Why?"

"Do know about how variables are actually used?"

"Try me."

"In logic, variables can be free, or bounded by quantifiers like 'for all', 'there exists', etc. If you take these variables and put them into a sentence, you have a propositional function. Substitute facts in for variables, and you have a proposition which has a truth-value: 0 for false or 1 for true."

"I'm with you so far."

"Now, although people like Carnap have postulated logics with no variables..."

The professor's eyes lit up.

"...a much more interesting variation is that, instead of having a fixed propositional function with a variable outcome depending on the facts you substitute into it, you have a fixed outcome, fixed facts, and a variable propositional function. Thus, having got the facts and the outcome (the outcome in this case being 1 or 0), you have an infinite number of situations that could give rise to them."

"Inductive rather than deductive logic?"

"Yes. You can start mucking around with things like universal propositions: in usual logic, these are propositions which are true no matter what you substitute in for the variables. In our logic, it means a fact that is valid for all possible generating logics. In fact, we'll have to change our terminology; propositional functions will get to be renamed prepositional functions."

"You're starting to get silly. What use is this?"

Richard thought for a moment. "Take Schrodinger," he said. "In normal logic, his cat was both dead and alive. Preposterous, obviously. But with this situational logic, the cat is definitely one or the other. It's simply that we don't know which situation is generating the fact of the cat being in whichever state it's in."

There was a pause for a moment.

"It almost sounds like you're talking about time going backwards," said the professor, still frowning.

"No," said Richard. "I'm simply talking about changing our perception of reality."

Another pause. The juke box started playing ABBA.

"But reality doesn't work like that," said the professor firmly, speaking slightly louder to get above the level of the music. "Things aren't just true or false. The statement 'that horrible machine over there..." The juke box was waved at. "...is going to play a song in E major exactly three days from now' is neither true nor false. It can't be, since to give it a value now would predict the future."

"True," said Richard immediately. "But multi-valued logic has been around for quite some time now - the Stoics and the Epicureans were concerned with it as early as 300BC, although only the Epicureans actually thought that the idea was useful since the Stoics were fiercely deterministic. However, it was only formalised by Lukasiewicz in 1918. Basically, the theory says that we can assign your statement a truth value of one half. As in, it might be true. Some have even suggested having an uncountable number of truth values, all between 0 and 1, in much the same style as probability, although obviously not doing quite the same job. You could start having things like the inferential quantifier: 'there might be an x such that...'. It's just that, obviously, neither contradiction nor the law of the excluded middle hold in multi-valued logic, so proof structures like reductio ad absurdam and infinite regress become impossible. Going back to your statement, its truth value would be nearer to one, I feel, since the juke box mainly plays rock music."

The professor stared into the distance in thought.

"But we're getting off the subject here," said Richard. "What we're trying to do is find out what, if anything, it is that time alternates between."

"I still don't quite believe you're taking this seriously," said the professor. "Even if our perception of time is logarithmic, and even if we can break down time into component Walsh functions, what would it achieve?"

"Well, to take the simplest example, the fundamental frequency could alternate between positive and negative logic." Richard saw the look on the professor's face. "Positive logic is where 1 is true, 0 is false, and negative logic is vice-versa, with 0 true and 1 false."

"No, no. I know what the difference is," muttered the professor, somewhat stunned. "It's just that that could explain something that's been puzzling me... You know my modulus box, and how I explained how it can tell if two objects are the same?"

"Yes."

"Well, I never actually explained how I make the objects disappear in the first place. Mainly because I didn't really know."

"You built the thing!"

"Yes, but the main component of it was, er, borrowed from that old laboratory across the road. You know, the one that was built with the university, before they added the extension that I'm in. I'd often wondered what it was, and then one day I came across some old papers, some of which tried to describe the equipment. They muttered something incomprehensible about making things negative, and talked about phase a lot. So I borrowed it, and found it could make things vanish. Controllably."

"Are you thinking what I'm thinking?" enquired Richard.

"I don't see why it shouldn't be the case," said the professor. "Simply shifting an object's truth value in positive and negative logic out of phase with time's frequency would suddenly make the object false. You'd have thought that would have made anything give up the will to exist."

"This is all rather too easy," said Richard dubiously. "It feels as if we've got something we don't know about, and are making up absurd theories to explain it."

"I thought that's how this situational logic worked," said the professor. Richard scowled heavily. "No, I mean it. Look, you've seen several odd things today. If inductive logic really does exist, then any explanation that could logically be derived from the facts is true."

"And I suppose you're going to say that, since I've set it up so that we can have harmonics of higher frequencies as well, we can have just about whatever we want being alternated."

"Yes, that's almost a problem," said the professor slowly. "I think we ought to go back to my lab to think about it. There might be something useful there."

Or there may not, thought Richard. He noticed the professor had already finished drinking and was putting on a coat. Richard decided that he wasn't about to drink his remaining half-pint in one go, and left it on the table, hurriedly putting on his own coat as the professor was nearly at the door.

The wind outside was definitely stronger now, and it was still drizzling. Richard caught up with the professor, and the two hurried back to the physics building. They climbed the stairs and finally got to the lab, where Richard sat down heavily and stared at the black boxes in a new way.

"Where were we?" asked the professor, taking Richard's coat and hanging it up to dry.

Richard expounded on what he'd been thinking on the way back. "I think we'd got as far as the fact that to make a periodic function from square waves you need an infinite series of Walsh functions, with the frequency tending to infinity as you get closer and closer to the original function. Which means there are an infinite number of things we can have alternating if we want."

"That sounds nasty. Anyway, surely we wouldn't need time modelled that accurately. Since we're only talking about our perception of it, and I don't believe that we could distinguish a rather, well, bumpy time from the real thing if the bumps were small enough, the series could stop once a suitable accuracy had been reached."

"The what?"

"Sorry?"

"The 'real thing'?"

"Oh. I see what you mean." The professor sighed. "This is all getting horribly complicated. We're starting to get back to Schrodinger in the sense of what is real and what we perceive."

"Well why don't we just have fun then?" asked Richard. "As long as we know we've got plenty of Walsh functions to play with, we can have endless discussions about what could alternate and the possible consequences."

The professor gave Richard a despairing look. Richard continued unabashed.

"Well look. We've got all sorts of logic systems: bivariate, multivariate,..."

"Non-variate!" exclaimed the professor, beaming at the LDEs.

"Inductive, deductive," continued Richard. "Positive, negative, relativistic, quantum..."

They both looked at each other.

"Where did that come from?" asked the professor.

"It's been a problem in logical philosophy for ages," said Richard. "Is everything pre-determined - also known as the clockwork universe theory, as you said earlier - or, since physics at the quantum level involves chance, can we never work out what's going to happen next? At the moment, there's a problem, because the former relativistic approach works at an everyday-and-bigger scale, whereas quantum physics only works at the sub-atomic level. They aren't compatible."

"And you're suggesting that time alternating between the two ways of doing things would be a good solution?"

"Can you see a problem with it?"

"Yes. The alternation is in itself deterministic."

"We just need some way of controlling the alternation."

"That would mean an infinite series of meta-logics, each controlling the one below."

"Why not?" concluded Richard.

The professor thought for a bit. Richard, although aware that the other mind in the room was rather better at the intricacies of quantum physics, was quietly hopeful that it couldn't come up with anything against his argument. Finally the eyes of the other mind lit up.

"If time really does work as you postulate..." said the professor. Richard wondered who had first come up with the idea of people's perception of time as logarithmic, but didn't say anything. "...Then it probably does solve the apparent incompatibilities between the systems. There is a slight problem, of course. We're basing this on your assumption of how time works, and unfortunately physics has generally regarded time as simply being another dimension - a fourth axis of reality."

"Except in certain superstring theories," interrupted Richard. "You seem to put a second time axis in there. Wouldn't that solve it, if time was a plane?"

"No. The second time dimension is simply a tool. Mathematicians put it there, actually - it helps unify certain equations. Nothing to do with quantum versus deterministic," added the professor hurriedly, as Richard started to look hopeful.

"So you're saying the theory doesn't work," said Richard, disappointedly.

"No, no. It's just that an awful lot of physics would have to be re-invented if time weren't an axis. And to be honest, the axis idea works very well. However, physics hasn't quite managed to work out the quantum-relativistic problem yet, so perhaps the rest of the world is wrong and we're right."

"I don't think I want to start calling the rest of the world wrong."

"Ah. That's what I've been thinking about. You see, I think I've just come up with an experiment that could test your theory."

"Really?" asked Richard. "When do we get to do it? How is it done? How does it work?"

"Yes, really," replied the professor calmly. "And as for how it works, well: simply put, the problem is that there is an incompatibility between quantum and relativistic physics. However, this boils down to one specific problem, namely unifying all four forces: gravitational, electromagnetic, strong and weak. You see, gravity is firmly in the realms of general relativity, whereas the other three are definitely quantum. So what physicists have been searching for for several decades now is a Grand Unified Theory, or GUT, that will unify all four forces together into one basic theory. A consequence of this being that we can prove that all universal constants, like Planck and such, are really universal, not man-made. A bit Platonic, you might say.

"How we do it is this. You know, I hope, about Heisenberg's uncertainty principle?"

"Yes. It's all about not being able to know a particle's exact momentum and exact position at the same time.'

"Absolutely - the more precisely you know one, the less precisely you know the other. It spawned a joke about physics students making the excuse that they determined the momentum of their homework so accurately that it could be anywhere in the universe. Anyway, my thinking goes like this.

"Heisenberg's equations come in two parts. If D means 'the uncertainty of', and h is Planck's constant, then the first part is DxDp > h/4p, where x is position and p is momentum. This basically means that if you're really certain about one of them - say you've got the error down to less than sqrt(h/4p) - then you simply can't be as certain about the other. However, there is also the part about energy, E, and time, t. This goes along much the same lines, namely DEDt > h/4p, although here the delta before the t really does mean the actual time, not the uncertainty of it.

"Now, the interesting thing is that if you get the actual energy on a particle high enough, the forces start unifying. The electromagnetic and the weak forces are the first to merge. Obviously strong will join after that, and finally - at an unimaginably high energy level - gravity will join. Thus, all we have to do is create a situation where, basically, there is infinite energy on a particle."

"All we have to do?" uttered Richard incredulously.

"Well, I think I've worked out a way. We need a large black box, and inside it a device that would measure a particle's position and an antinomialist computer. Oh, and of course a modulus box needs to be in there as well to reduce an area of space to a single particle."

"What's the plan?" asked Richard, not quite believing that there would be one.

"Simple," came the reply. "The theory works because of frames of reference. It was postulated by Newton that if you are going to get sensible results, you need a non-accelerating frame of reference. Non-accelerating, that is, with respect to any forces or particles you're measuring. "Now, if in our black box we measure the position of the particle, then that position is known with reference to the lab. In fact, we could make the frame of reference hinge around the position of the particle at that point, say make its position the origin. That wouldn't make any difference in a normal situation. However, what we do is to feed the exact position of that particle into the computer."

The professor paused to let Richard work out the consequences himself.

"But the position would have to be fed in as a variable," said Richard at last.

"Not exactly. We would lose the number by utilising a transitional variable. Just as the example in the essay lost the number seventy-three, we could lose, within the confines of the black box we're working in, the origin of the frame of reference."

"It seems to me that what you're doing is, well, sort of deliberately and specifically not measuring the particle's position."

"That's right," beamed the professor. "With the consequence that the frame of reference disappears."

"But, but, b..." stammered Richard. "Why???"

"Because then we've got a rather lost particle. Obviously it has to have some sort of frame of reference, so it should sort of 'inherit' the universe itself as a frame of reference."

Richard raised an eyebrow so hard it almost vanished into his hair. "That's not really answering my question," he said firmly.

"Well, you see, remember Heisenberg's equations? What I'm trying to do is to make h/4p exact."

"Of course it's exact. Planck's constant and pi are universal constants."

"Ah, but in the lab, and any frame of reference generated within it, because Heisenberg's equations are all about measurement we have to use our own measurements of those constants, which are far from accurate."

"Pi is known to about 10-to-the-10 decimal places," complained Richard.

"But we need it infinitely accurately - we need the Perfect Pi. And of course, the only way to get that is to adopt the universe's frame of reference. It'll only exist inside the black box, of course, but that's exactly where we need it. Planck's constant will be perfect inside there as well."

"Why do we need them perfectly?" protested Richard again, but it fell on deaf ears. The professor had been busy rummaging during the conversation, and the ears were now buried under several layers of boxes as the search continued. Finally the search came to and end, and the professor came backwards out of the corner of the room dragging a large piece of equipment.

"What's that?" asked Richard.

"A particle detector," replied the professor.

"You mean we're actually going to do this experiment now?" asked Richard. "I still haven't understood it, and I'm not sure I want to be in the same room as an experiment of yours that I don't understand."

"It's perfectly safe," the professor reassured him.

"Weren't you just, er, talking about infinite energy a moment ago?"

"It's perfectly safe, trust me."

Richard really couldn't bring himself to. He looked pleadingly at the professor.

"Oh, all right, I'll explain it to you," said the professor after a few moment's thought. "Inside this large black box we'll have created the situation whereby h/4p is absolutely precise. Useless on its own, of course, but there's more.

"Remember that DE is the uncertainty of the energy of the particle. It's a very useful notation, just like dx/dy in calculus, because although it shouldn't be split into two, in some circumstances you can. So all we have to do is divide the equation DEDt > h/4p through by the uncertainty. Of course, uncertainty is always going to be positive, so there's no need to worry about changing the direction of the inequality."

"You're seriously suggesting dividing Heisenberg's equation through by 'uncertainty'?"

"Why not? Then, because pi is known exactly, D(4p) is going to be zero."

"But that gives us h divided by 0. Which is undefined. It's infinite."

"So the consequences are...?"

"Well... ." Richard's entire face collapsed in despair at this insane situation. "I suppose what you're driving at is that EDt also has to be infinite, and since the time taken to do the experiment won't be infinite, the energy itself has to be." Richard thought through the situation again, and started to wonder if it might be plausible after all.

By this time the professor had found six large pieces of plastic, which were obviously designed to assemble together into a black box that was about two metres long and one metre along the other sides. The box was assembled around the particle detector. Richard suddenly had a nagging doubt.

"Aren't particle detectors large, aircraft hangar-filling devices?" he asked.

"Usually, yes. They use the space for detecting all the really energetic particles like muons, but we don't need that. I thought we'd do this experiment with an electron. Umm, could you give me a hand with the modulus box, please?"

They lifted the smaller box into the larger box. The professor fiddled with the positioning for a while, leaving Richard to wander round the room looking at things. Another thought came to him.

"I rather gained the impression that you hadn't actually got around to actually building an antinomialist computer yet," he said.

"Oh yes," came the muffled reply. The professor stopped fiddling and stood up straight. "I've built a couple of prototypes that really are antinomialist, it's just that they have very few components and rather limited input and output. But that's not a problem for this purpose."

The professor went back to setting up the particle detector to coincide with the contents of the modulus-field inducer. After about five minutes everything was done, and the professor asked Richard to help to move the computer inside the box. They heaved it in, and various wires were connected up. Finally a large battery pack was put into the far corner of the box and things were plugged into it. Richard realised that connecting the equipment to the mains might count as communication with the outside world and would therefore spoil the experiment. Soon the professor seemed satisfied that everything was ready. The lid was put on the box and fastened down securely. Richard noticed that the whole thing had been designed to be basically seamless. It appeared absolutely smooth, with no trace of joins, and certainly no gaps where the sides met. Beautifully designed, he thought. The professor interrupted Richard's observations with a slight cough.

"All ready to go?" asked Richard.

"Yes. I think so."

Richard still couldn't quite believe they were doing this. If a bizarre and rather twisted piece of reasoning actually worked, they would shortly be giving infinite energy to an unsuspecting electron contained in a box no bigger than two cubic metres. If it didn't blow most of the lab (or Earth, or solar system) apart, when they opened the lid at the end they would have a Grand Unified Theory. He gazed out of the window hoping that somehow everything could make sense to him. The wind and rain had eased off a little, he noticed. Another cough indicated that everything was finally ready.

The professor pressed a switch that was fitted onto the far side of the box.

Richard stared at it. "Is it working?" he asked. He couldn't see or hear any signs of anything happening.

"Oh yes," replied the professor. "The whole thing is totally sealed. By now only a single electron is in the box, and it'll be detected any second now. It'll be a few seconds before the computer manages to lose its position, though, it's a rather early version."

Richard stared on in wonder. About twenty seconds passed. All the feelings and tinglings of excitement welled up inside him, and he wondered how much longer it would be before everything was over. At last the silence was broken.

"Well, we should have unified all the forces by now," said the professor, rather too matter-of-factly for Richard's liking. "Now we simply have to measure the properties of the electron and we've got a GUT."

"May I open the box?" asked Richard, slightly suspiciously. After all this excitement, he wanted to make sure it was all real.

"Certainly," replied the professor. "Just push this catch here and lift the lid."

Richard stepped forwards to the box. He had his hand on the catch and was just about to open it, when a thought struck him with as much force as a falling brick. He leapt back with a silent yelp. Of all the things that could have happened, he thought, didn't it just have to be this.

"Hang on," he said, shaking. "The whole thing depends on not having the lab as a frame of reference." The professor looked up sharply. "If it did, the uncertainty of the value of pi would be far too large - over 10-to-the-minus-10. The energy on the electron wouldn't even be enough for the first two forces to unify."

The professor blinked. "You mean we've already found the answer, we just can't know what it is?"

Richard nodded gently. "We've got a GUT, only if we try and actually find out what it is, we don't have one any more."

"I think I'll just go and fill in my next research grant application," mumbled the professor, and walked out of the room slowly. Richard quietly went over to the box and turned it off before leaving as well, closing the door silently behind him.















© Copyright Oliver Humpage, 25/1/99.